Statistical Analysis: Partial Effects & Oaxaca Decomposition
Partial effects can be computed automatically for any variable in any model regardless of how intricate. Oaxaca decomposition can be used for any model fit by the program, not just linear regression.
Partial Effects Reported
- Compute for all models with conditional mean functions
- Average effects
- Compute at means and at specified points
- Compute at specified strata
- List estimates and standard errors
- Compute for specified scenarios
- Appropriately account for interaction terms and nonlinearities
Dummy Variables
Partial effects distinguish between dummy variables and continuous variables. For a dummy variable, the effect is computed as the difference in the estimated probabilities with the dummy variable equal to one and zero and other variables at their means. For continuous variables, the effect is the derivative. The program also computes elasticities.
Example - Partial Effects
The following first estimates an ordered probit model for health satisfaction. The variable is coded 0-10, so there are 11 outcomes. The specification involves some nonlinearity, two interaction terms and two dummy variables, one of which is interacted with income.
HSAT* = b1 + b2*age + b3*age*age + b4*educ + b5*married + b6*female + b7*hhninc + b8*female*hhninc
-----------------------------------------------------------------------------
Ordered Probability Model
Dependent variable HSAT
Log likelihood function -56863.29478
Restricted log likelihood -57836.42214
Chi squared [ 8 d.f.] 1946.25471
Significance level .00000
McFadden Pseudo R-squared .0168255
Estimation based on N = 27326, K = 18
Inf.Cr.AIC = 113762.6 AIC/N = 4.163
Underlying probabilities based on Normal
--------+--------------------------------------------------------------------
| Standard Prob. 95% Confidence
HSAT| Coefficient Error z |z|>Z* Interval
--------+--------------------------------------------------------------------
|Index function for probability
Constant| 2.94117*** .10632 27.66 .0000 2.73279 3.14955
AGE| -.03456*** .00486 -7.11 .0000 -.04409 -.02503
AGE^2.0| .00013** .5466D-04 2.38 .0175 .00002 .00024
EDUC| .03494*** .00287 12.16 .0000 .02931 .04057
MARRIED| .05965*** .01548 3.85 .0001 .02932 .08999
FEMALE| -.19219*** .05572 -3.45 .0006 -.30140 -.08298
|Interaction FEMALE*AGE
Intrct02| .00361*** .00111 3.25 .0012 .00143 .00578
HHNINC| .28787*** .05138 5.60 .0000 .18718 .38857
|Interaction HHNINC*FEMALE
Intrct03| -.05835 .07056 -.83 .4083 -.19665 .07995
|Threshold parameters for index
Mu(1)| .19362*** .01003 19.30 .0000 .17396 .21328
Mu(2)| .49967*** .01088 45.94 .0000 .47835 .52099
Mu(3)| .83603*** .00990 84.41 .0000 .81661 .85544
Mu(4)| 1.10537*** .00909 121.66 .0000 1.08756 1.12317
Mu(5)| 1.66272*** .00801 207.52 .0000 1.64702 1.67843
Mu(6)| 1.93147*** .00774 249.57 .0000 1.91630 1.94664
Mu(7)| 2.33904*** .00777 301.05 .0000 2.32381 2.35427
Mu(8)| 2.99472*** .00851 351.84 .0000 2.97804 3.01140
Mu(9)| 3.45408*** .01018 339.45 .0000 3.43414 3.47402
--------+--------------------------------------------------------------------
Note: nnnnn.D-xx or D+xx => multiply by 10 to -xx or +xx.
Note: ***, **, * ==> Significance at 1%, 5%, 10% level.
-----------------------------------------------------------------------------
Partial effects are first computed for all variables of the probability that the health satisfaction is reported as 7.
PARTIALS ; Effects: age / educ / married / female / hhninc
; Outcome = 7 $
---------------------------------------------------------------------
Partial Effects Analysis for Ordered Probit Prob[Y = 7]
---------------------------------------------------------------------
Effects on function with respect to AGE
Results are computed by average over sample observations
Partial effects for continuous AGE computed by differentiation
Partial effects for continuous EDUC computed by differentiation
Partial effects for binary var MARRIED computed by first difference
Partial effects for binary var FEMALE computed by first difference
Partial effects for continuous HHNINC computed by differentiation
* ==> Partial Effect for a Binary Variable
---------------------------------------------------------------------
Partial Standard
(Delta method) Effect Error |t| 95% Confidence Interval
---------------------------------------------------------------------
AGE .00037 .00005 7.10 .00027 .00048
EDUC -.00040 .00005 8.15 -.00050 -.00031
* MARRIED -.00055 .00012 4.44 -.00079 -.00031
* FEMALE .00224 .00051 4.42 .00125 .00324
HHNINC -.00326 .00061 5.30 -.00446 -.00205
---------------------------------------------------------------------
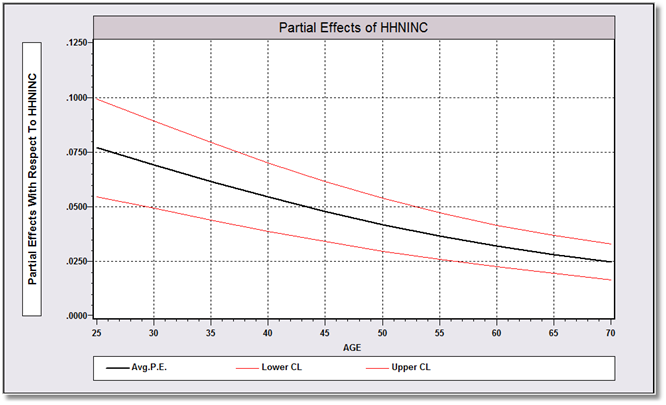
The data set is a panel observed yearly from 1984-1991. We restrict our sample to the 1991 wave, and compute average partial effects for income fixing age at 25, 30, .., 70, then plot the results as a function of age with a confidence interval around the estimated average partial effects at each age.
REJECT ; year # 1994 $ PARTIALS ; Effects: hhninc & age = 25(5)70 ; Plot(ci)$ --------------------------------------------------------------------- Partial Effects Analysis for Ordered Probit Prob[Y = 10] --------------------------------------------------------------------- Effects on function with respect to HHNINC Results are computed by average over sample observations Partial effects for continuous HHNINC computed by differentiation Effect is computed as derivative = df(.)/dx --------------------------------------------------------------------- df/dHHNINC Partial Standard (Delta method) Effect Error |t| 95% Confidence Interval --------------------------------------------------------------------- APE. Function .05261 .00780 6.74 .03732 .06790 AGE = 25.00 .07677 .01140 6.73 .05443 .09912 AGE = 30.00 .06900 .01020 6.76 .04901 .08900 AGE = 35.00 .06139 .00905 6.78 .04365 .07914 AGE = 40.00 .05419 .00799 6.78 .03853 .06986 AGE = 45.00 .04758 .00704 6.76 .03379 .06137 AGE = 50.00 .04163 .00619 6.72 .02949 .05376 AGE = 55.00 .03637 .00546 6.66 .02566 .04708 AGE = 60.00 .03180 .00487 6.53 .02225 .04134 AGE = 65.00 .02786 .00442 6.30 .01920 .03653 AGE = 70.00 .02452 .00413 5.94 .01642 .03261
Example - Oaxaca Decomposition
We continue the preceding example by decomposing the ordered probit model results for two subsamples, working and nonworking individuals. This takes two steps. In the first, the model is estimated for the two groups and (again) for the pooled sample.
ORDERED ; For [working=*,0,1]
; Lhs = hsat ; Rhs = one, age, age^2, educ, married, female,
female*age, hhninc, hhninc*female $
(We’ve omitted the three sets of estimation results.) The simple command
DECOMPOSE $
produces the decomposition.
-----------------------------------------------------
Setting up an iteration over the values of WORKING
The model command will be executed for 2 values
of this variable. In the current sample of 3377
observations, the following counts were found:
Subsample Observations Subsample Observations
WORKING = 0 939 WORKING = 1 2438
WORKING =**** 3377
----------------------------------------------------
Actual subsamples may be smaller if missing values
are being bypassed. Subsamples with 0 observations
will be bypassed.
-----------------------------------------------------------------
Subsample analyzed for this command is WORKING = 0
-----------------------------------------------------------------
Subsample analyzed for this command is WORKING = 1
-----------------------------------------------------------------
Full pooled sample is used for this iteration.
-----------------------------------------------------------------
-------------------------------------------------------------------
Decomposition of Changes in Average Functions
Model Used in Computations = Ordered Probit Prob[Y = 10]
-------------------------------------------------------------------
Sample is WORKING = 0 WORKING = 1 Sample
Estimates Based on (0) (1) Size
WORKING = 0 (a) .053819 (a,0) .068907 (a,1) 939
WORKING = 1 (b) .059630 (b,0) .083887 (b,1) 2438
Pooled =** (*) .056810 (*,0) .082953 (*,1) 3377
-------------------------------------------------------------------
Wald Test of Difference in the Two Coefficient Vectors
Chi squared[ 18] = 103.2028 , P Value = .0000
-------------------------------------------------------------------
Total Change in Function (a,0) - (b,1) = -.030068 ( 100.00%)
-------------------------------------------------------------------
Oaxaca | Due to data is (a,0) - (a,1) = -.015088 ( 50.18%)
Blinder | Due to beta is (a,1) - (b,1) = -.014980 ( 49.82%)
-------------------------------------------------------------------
Daymont | Due to data is (b,0) - (b,1) = -.024258 ( 80.68%)
Andrisani | Due to beta is (a,0) - (b,0) = -.005810 ( 19.32%)
-------------------------------------------------------------------
Daymont | Due to data is (b,0) - (b,1) = -.024258 ( 80.68%)
Andrisani | Due to beta is (a,1) - (b,1) = -.014980 ( 49.82%)
(3 Fold) | Due to function (a,0) - (b,0) -
| (a,1) - (b,1) = .009170 ( -30.50%)
-------------------------------------------------------------------
Ransom | Due to data is (*,0) - (*,1) = -.026144 ( 86.95%)
Oaxaca | Due to beta is (a,0) - (*,0) + -.003925 ( 13.05%)
Neumark | (*,1) - (b,1)
-------------------------------------------------------------------

